What Is an Annuity?
An annuity is a series of equal payments made at equal intervals. Annuity payments don’t have to be made annually but can be made monthly, weekly, or even daily. The critical factors are:
- The payments equal to each other and;
- The interval between the payments is the same.
An ordinary annuity is the one in which payments are made at the end of each period. The formula for calculating present value of ordinary annuity can be written as
\[\begin{matrix}P{{V}_{annuity}}=PMT\times \frac{1-\frac{1}{{{\left( 1+i \right)}^{n}}}}{i} & {} & \left( 1 \right) \\\end{matrix}\]
Where
PMT=the periodic payment in the annuity
i=the interest rate
n= the number of payments
The term after the multiplication sign in Eq. 1 is the present value interest factor for an annuity (FVIFA).
\[\begin{matrix}PVIF{{A}_{i,n}}=\frac{1-\frac{1}{{{\left( 1+i \right)}^{n}}}}{i} & {} & \left( 2 \right) \\\end{matrix}\]
Example PV of Ordinary Annuity
Say you have won the lottery! The prize is $100 paid at the end of each of the next four years. What would be the present value of the lottery annuity if the interest rate is 10%?
Solution
\[\begin{align} & PMT=\$100\\&i=0.1\\&n=4\\\end{align}\]
This question asks for the future value of an ordinary annuity, so
\[\begin{align}& P{{V}_{annuity}}=PMT\times PVIF{{A}_{i,n}} \\& PVIF{{A}_{i,n}}=\frac{1-\frac{1}{{{\left( 1+0.10 \right)}^{4}}}}{0.10}=3.16987 \\& P{{V}_{annuity}}=100\times 3.16987=\$316.99\\\end{align}\]
We’ve just discovered that the present value of a four-period stream of $100 cash flows is $316.99. This is the present value of the lottery prize. You would be indifferent between the four payments of $100 or a 316.99 to invest today, then it has just enough money to fund each of the $100 payouts. The government treasurer could invest the $316.99 at 10% and have $348.69 1 year later. The first $100 prize is then subtracted from the balance, which is reinvested.
One year later, the balance is $273.56 and an additional $100 is subtracted. This process continues as shown in Figure 1 until the final $100 is subtracted and the remaining balance is zero.
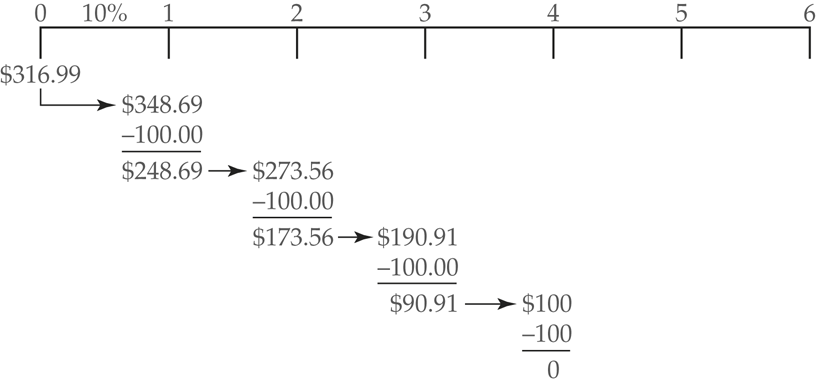
Figure 1
This example provides an important clue as to when you’ll want to use present value equations. Anytime you want to know how much you need today to create a future cash flow stream, find the present value of the cash flows.