Simple interest is easy to compute, but most of the time, we want our interest payments to be reinvested. For example, if you put money into your bank savings account, the bank routinely deposits the monthly or quarterly interest payments back into your account. During following periods, interest is earned on a higher balance. If the interest is reinvested, then, in later periods, interest is made on earlier interest. This is compound interest.
Virtually all of the calculations performed in finance assume that interest is compounded. We begin our study of compound interest by finding future balances over multiple periods with annual compounding.
Compound Interest: Future Value over One Year
As we saw in the introduction, if you make a $100 deposit into a bank that pays 5% interest once per year, you’ll have $105 at the end of 1 year. The formula for computing the balance after one period is given in the following equation:
\[\begin{align}& F{{V}_{1}}=P{{V}_{0}}\times (1+i) \\& F{{V}_{1}}=\$100\times(1+0.05)=\$105\\\end{align}\]
This calculation is shown on the timeline in Figure 1. At time period 0, we see a present value of 105. Notice the use of the subscripts in the above formula. The subscript denotes the point on the timeline when the cash flow occurs.
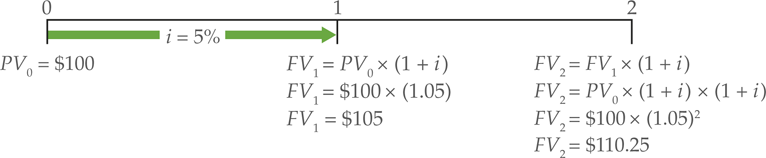
Figure 1: Future Value over a period of time
Compound Interest: Future Value over Two Years
Now suppose that you leave the deposit in the bank to compound for another year, without withdrawing any money. Using the above formula, the balance grows to $110.25:
\[\begin{align}& F{{V}_{2}}=F{{V}_{1}}\times (1+i) \\& F{{V}_{2}}=\$105\times(1+0.05)=\$110.25\\\end{align}\]
This calculation is shown under period 2 on the timeline in Figure 1.
For the period of first year, the account earned $5, but during the second year, it earned $5.25. The extra 5.00×0.05=$0.25)—it is compound interest. We can streamline these calculations by observing that FV1 is equal to PV0× (1+i) and then by substituting PV0× (1+i) for FV1 into the equation as given below:
\[\begin{align}& F{{V}_{2}}=P{{V}_{0}}\times (1+i)(1+i) \\& F{{V}_{2}}=P{{V}_{0}}\times {{(1+i)}^{2}} \\& F{{V}_{2}}=\$100\times{{(1+0.05)}^{2}}\\&F{{V}_{2}}=\$100\times1.1025=\$110.25\\\end{align}\]
The process of calculating a future balance over multiple periods is termed as compounding because the investor is receiving compound interest.
Compound Interest: Future Value over Multiple Years
Similarly, each subsequent period of compounding increases the exponent by one. The equation to find the future value of a deposit is
\[F{{V}_{n~}}=~P{{V}_{0}}~\times ~{{(1+i)}^{n}}\]
Where
FVn=the future value of a deposit at the end of the nth period
PV0=the initial deposit
i=the interest rate earned during each period
n= the number of periods the deposit is allowed to compound
Let’s illustrate with an example.
Example 1: Future Value over Multiple Years
Suppose your grandfather gave you $1000 when you graduated from college. Instead of using it to buy clothes, you decided to invest it and to not touch the balance for 40 years, until you retire. If you managed to earn 10% per year, what is the future value of your investment?
Solution
To work out the future value of 1000 over 40 years compounded at 10:
\[F{{V}_{n}}=P{{V}_{0}}\times {{(1+i)}^{n}}\]
\[\begin{align}&F{{V}_{40}}=\$1,000\times{{(1.10)}^{40}}\\&F{{V}_{40}}=\$1,000\times45.25926\\&F{{V}_{40}}=\$45,259.26\\\end{align}\]
Calculating Interest Earned
For finding the interest earned, we subtract the principal (which is the original amount) from the ending balance as shown below:
\[\begin{align}& Interest~earned=FV-PV \\& Interest~earned=\$45,259.26-\$1,000=\$44,259.26\\\end{align}\]
Simple and Compound Interest Compared
If simple interest, rather than compound interest, had been earned in Example 1, then$100 per year would have been earned 100. Over a period of 40 years, the total simple interest earned would have been 40 times $100 or $4,000. Since the total amount of interest earned was $44,259.26, the difference 4,000 of $40,259.26 was earned because of compounding. Put another way, $40,259.26 in interest was earned on interest.
In this example, more interest was earned on the interest than was earned on the original principal! This is the magic of compound interest.
Compounding Rules of Thumb
Here are some rules that will help you think of the theory of compound interest in more meaningful ways.
Future balance increases if periods and/or interest rates increase.
First, as the number of compounding periods increases, the future balance increases. Second, as the interest rate increases, the future balance increases.
Compound interest theory applies to any growth.
One of the more important features of TVM calculations is that the methods can be applied to anything that grows. We can use the same equations to find future sales, if sales grow at a constant rate. The method can be applied to any constant growth situation, whether it be money, sales, profits, or dividends.
Any length of period can be used.
Time does not have to be measured in years. The formula can be used with any length period: days, weeks, months, quarters, or years. This period is called the compounding period or the conversion period. This period is the basic unit of time in all time value of money problems. However, whatever compounding period is used, the interest rate must be defined over the same period.