What Is an Annuity?
An annuity is a series of equal payments made at equal intervals. Annuity payments don’t have to be made annually but can be made monthly, weekly, or even daily. The critical factors are:
- The payments equal each other and;
- The interval between the payments is the same.
Ordinary annuity is the one in which payments are made at the end of each period.
Example
Assume you would like to know the future balance in your interest-bearing bank account 3 years later if you make three yearly $100 deposits. We’ll suppose that your bank pays interest at the rate of 10% each year. The timeline of cash flows is demonstrated in Figure 1.

Figure 1: Timeline of Cash Flow
The “long” approach finds the future value of each cash flow and adds them up as shown in Figure 2. The values shown under date 3 on the timeline are just the future value of each corresponding cash flow.
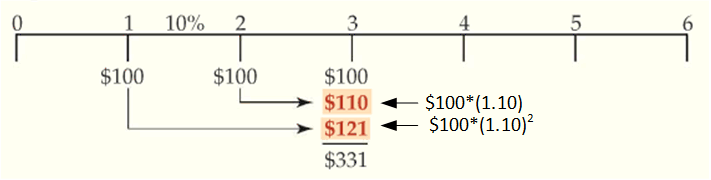
Figure 2: Future Value of each Cash Flow
The total future value would be the sum of the future values for each individual payment, so we can demonstrate the future value of the ordinary annuity as follow:
\[F{{V}_{annuity}}=PM{{T}_{1}}\times {{\left( 1+i \right)}^{n-1}}+PM{{T}_{2}}\times {{\left( 1+i \right)}^{n-2}}+\cdots +PM{{T}_{n-1}}\times {{\left( 1+i \right)}^{1}}+PM{{T}_{n}}\times {{\left( 1+i \right)}^{0}}\]
After some algebra, the formula can be simplified to:
\[\begin{matrix} F{{V}_{annuity}}=PMT\times \frac{{{\left( 1+i \right)}^{n}}-1}{i} & \left( 1 \right) \\\end{matrix}\]
Where
PMT=the periodic payment in the annuity
i=the interest rate
n= the number of payments
The term after the multiplication sign in Formula 1 is the future value interest factor for an annuity (FVIFA).
\[\begin{matrix} FVIF{{A}_{i,n}}=\frac{{{\left( 1+i \right)}^{n}}-1}{i} & \left( 2 \right) \\\end{matrix}\]
Example 1 Future Value of an Ordinary Annuity
Let’s suppose you won the lottery. The prize-money comprises 20 equal annual payments of $50,000. You choose to save all of this prize-money for your retirement, and you deposit all the money into an account that makes 8% per year. What is the amount of your retirement nest egg?
Solution
The example gives us the following information:
\[\begin{align}& PMT=50,000 \\& i=0.08 \\& n=20 \\\end{align}\]
This question asks for the future value of an ordinary annuity, so
\[\begin{align}& F{{V}_{annuity}}=PMT\times FVIF{{A}_{i,n}} \\& FVIF{{A}_{i,n}}=\frac{{{\left( 1+0.08 \right)}^{20}}-1}{0.08}=45.76196 \\& F{{V}_{annuity}}=50,000\times 45.76196=\$2,288,098.21\\\end{align}\]
The future value of an annuity is very sensitive to changes in the interest rate.