Interest Rate Calculation Formula
Here, we’ll use a future value equation to solve for how much a deposit today can grow to in the future. There are times, however, when we already know both the future and present values and want to know either the interest rate or the number of time periods it took to earn the future balance.
We can use the following formula to solve for the interest rate (when it is the unknown):
\[\begin{align}& F{{V}_{n}}=P{{V}_{0}}\times {{\left( 1+i \right)}^{n}} \\& {}^{F{{V}_{n}}}/{}_{P{{V}_{0}}}={{\left( 1+i \right)}^{n}} \\& {{\left[ {}^{F{{V}_{n}}}/{}_{P{{V}_{0}}} \right]}^{{}^{1}/{}_{n}}}={{\left[ {{\left( 1+i \right)}^{n}} \right]}^{{}^{1}/{}_{n}}}=\left( 1+i \right) \\& i={{\left[ {}^{F{{V}_{n}}}/{}_{P{{V}_{0}}} \right]}^{{}^{1}/{}_{n}}}-1 \\\end{align}\]
Example 1 Future Value, Solving for the Interest Rate
Just as you were about to enter college, you discovered that a great uncle had established an education trust fund for you when you were born, 20 years ago. He made a deposit of $5,000 in the beginning. If the total balance is now $19,348.42, what average compounded rate of return has been earned?
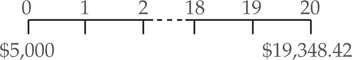
We can use the following equation to solve for the unknown interest rate:
\[i={{\left[ {}^{F{{V}_{n}}}/{}_{P{{V}_{0}}} \right]}^{{}^{1}/{}_{n}}}-1={{\left[ {}^{19,348.42}/{}_{5,000} \right]}^{{}^{1}/{}_{20}}}-1=7%\]
Number of Time Periods Calculation Formula
If you know the PV, FV, and the interest rate you can compute the number of time periods.
Example 2 Future Value, Solving for n
How long will it take to double the money at 3% interest rate? For instance, if inflation averages 3% per annum, then total how many years will it take for the price of a pint of beer to double from $1.50 to $3.00?
Solution
\[\begin{align} & P{{V}_{0}}=\$1.50\\&F{{V}_{0}}=\$3\\&n=?\\&i=0.03\\\end{align}\]
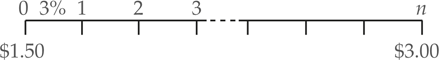
First, we set this up as a future value problem where the unknown is the number of compounding periods, n:
\[\begin{align}& F{{V}_{n}}=P{{V}_{0}}\times {{\left( 1+i \right)}^{n}} \\& {}^{F{{V}_{n}}}/{}_{P{{V}_{0}}}={{\left( 1+i \right)}^{n}} \\& n=\frac{\ln \left( {}^{F{{V}_{n}}}/{}_{P{{V}_{0}}} \right)}{\ln \left( 1+i \right)} \\\end{align}\]
The excel sheet above shows how to solve for n when other variables are known.